【統計学】分散・標準偏差とは?関数で簡単に求める【Excel】
当ページのリンクには広告が含まれています。
統計学の基礎知識である「分散・標準偏差」。
データのまとまりから数値の散らばり具合を見る言葉です。
例えば、ある数値の集合体
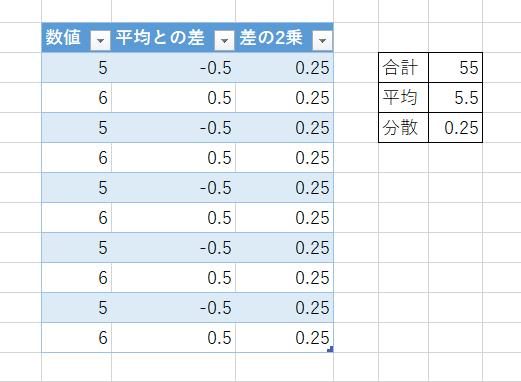
- 5,6,5,6,5,6,5,6
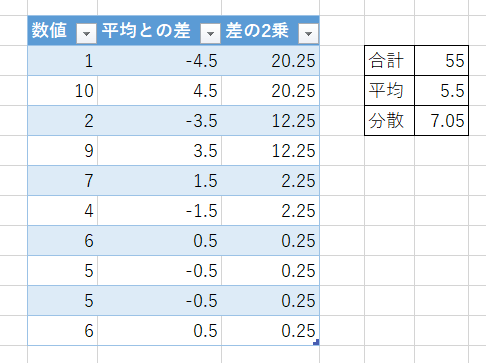
- 1,10,2,9,7,4,6,5,5,6
どちらも平均値は「5.5」になりますが、データの性質としては異なるものと感じませんか?
これを数値化するのが「分散・標準偏差」です。
あわせて読みたい


【統計学】記述統計量のまとめ(平均・分散・標準偏差・変動係数・共分散・相関係数)
記述統計での頻出の用語・公式をまとめました。 平均(average) 平均の公式 母集団の平均 = 標本の平均 = 説明 サンプル数nを合計して、nの数で割ったもの。 補足 は始…
目次
分散とは?
分散とは、単純なデータの散らばり具合を見るための指標です。
計算方法は
- データの平均値を取得
- 各データから平均値を引いて2乗する
- ②のデータをすべて足す
- データ数で割る
このようになります。
Excelで先ほどのサンプルデータを使って求めてみます。
まずは「5,6,5,6,5,6,5,6」から見てみましょう。
分散の公式
分散 = (( データ – 平均値 )²) の総和 ÷ データ数
平均値が5.5、全て値の平均との差-0.5を2乗し、データの個数10で割ると、分散は0.25となります。
次は「1,10,2,9,7,4,6,5」で見てみます。

分散は7.05になりました。
2乗する理由は?
平均との差はプラス・マイナス両方の値が考えられるため、数値とするため2乗しています。
標準偏差とは?
分散は、計算するために2乗しているためデータが大きくなり単位が異なります。これを正すために平方根を取り、単位を揃えます。
標準偏差の公式
標準偏差 = √分散
先ほど求めた分散に当てはめると
- 0.5(標準偏差) = √0.25(分散)
- 2.65(標準偏差) = √7.05(分散)
となりました。
なぜ標準偏差を求めるのか?
標準偏差を求めることにより、データが正規分布に従っていると仮定して、データ範囲内の数値が現れる確率を求めることができます。
この考え方が統計学の基礎となります。
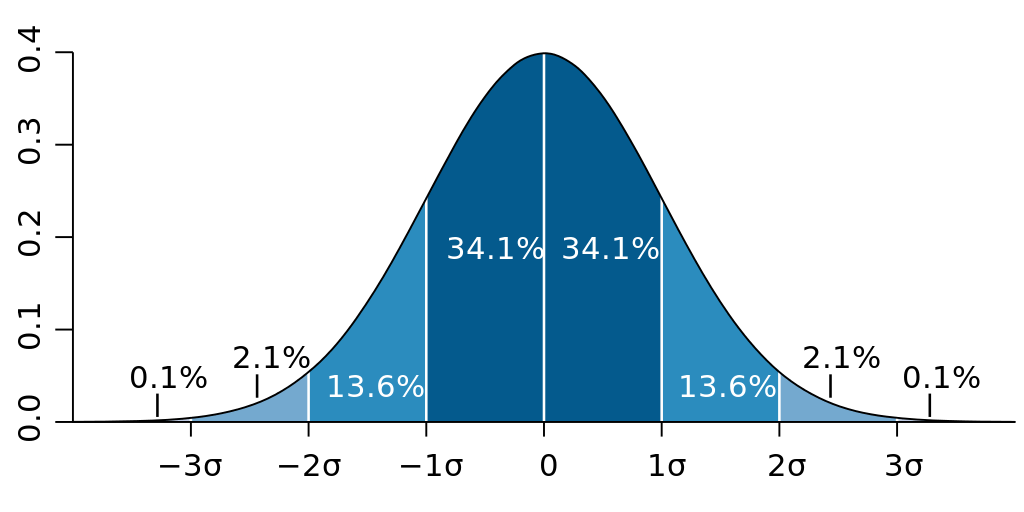
上記図は見ると、平均値を0として平均値±標準偏差で68.2%の確立と算出できます。
他には平均値±標準偏差×3(3α)で見ると99.7%とほとんどを網羅することができます。
| 範囲 | 指定した値が出現する確率 | 標準偏差:0.5の範囲 | 標準偏差:2.65の場合 |
|---|---|---|---|
| 平均値±標準偏差 | 68.3% | 5~6 | 2.85~8.15 |
| 平均値±(標準偏差×2) | 95.4% | 4.5~6.5 | 0.2×10.8 |
| 平均値±(標準偏差×3) | 99.7% | 4~7 | -2.45~13.45 |
あわせて読みたい

【Excel】記述統計量が簡単に確認できる分析ツールの使い方
記述統計とは、最大値や平均・中央値などを求め、データの特徴を確認することを言います。 データ分析の際には、必須作業でありデータの分布状況を把握するのに役立ちま…
あわせて読みたい


【推測統計】頻出の用語・公式まとめ【inferential statistics】
推測統計とは、標本のデータから母集団を予測する際に使われる考え方をいいます。 確率分布(probability distribution) 分布とは、ある事象が起こりえる頻度(確…

コメント