【確率】確率分布の種類まとめ【離散分布・連続分布】

確率変数と確率分布とは
確率変数
例えば、サイコロを投げて出る目は1~6のいずれかになり、それぞれの目が出る確率は\(\frac{1}{6}\)となります。この、サイコロを投げて出る目を「確率変数」であると言えます。
サイコロの出る目を確率変数の値としてXとおくと、下記のように表すことが出来ます。
\(P(X) = \frac{1}{6} (X = 1,2,3,4,5,6)\)
確率分布

確率変数で紹介した、サイコロの目の例で考えてみましょう。
サイコロの1~6が出る確率は全て\(\frac{1}{6}\)となるので
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 確率 | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) | \(\frac{1}{6}\) |
この表を図示すると
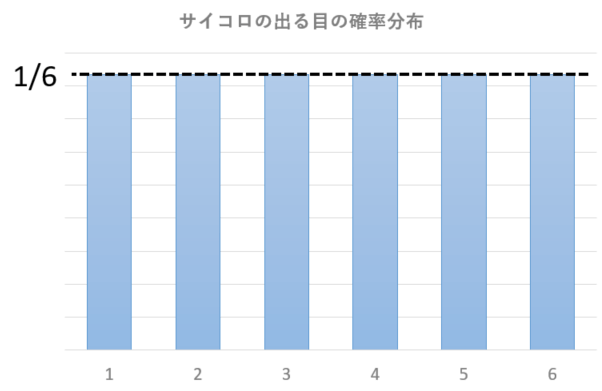
このようになります。
サイコロの出る目の確率は全て同じですので一様に分布しています。
確率変数によって確率が変化する確率分布など、複数の確率分布があるので、ご紹介いたします。
\(X \sim N (\mu,\sigma^2)\)
Xが変数、Nが分布の種類を表現しており、()内がその分布の特徴(パラメーター)を示しています。
これからご紹介する分布には、それぞれの分布の表記方法を合わせてご紹介します。
確率分布の二種類のカテゴリ
確率分布は大きく分けると二種類のカテゴリに分けられます。
- 離散分布
- 連続分布
離散分布
- 有限の結果
- 区間の確立を求める場合には、それらの要素を足していく
- グラフは棒グラフのような形になる
連続分布
- 無限の結果
- 数が無限であることから、個別の確立を足すことは出来ない
- 図や連続した関数で表現することができ、なめらかな曲線になる
離散分布の種類
| 離散分布の種類 | 意味 |
|---|---|
| 一様分布 | 結果が同様に確からしい場合(等確率) |
| ベルヌーイ分布 | 起こりえる結果が二つの事象のみ(YES・NO) |
| 二項分布 | 同様の実験を複数回行う場合 (ベルヌーイ事象を繰り返し行った場合) |
| ポアソン分布 | 与えられた期間に、事象が特定の回数発生する確率 |
一様分布
\(X \sim U(a,b)\)
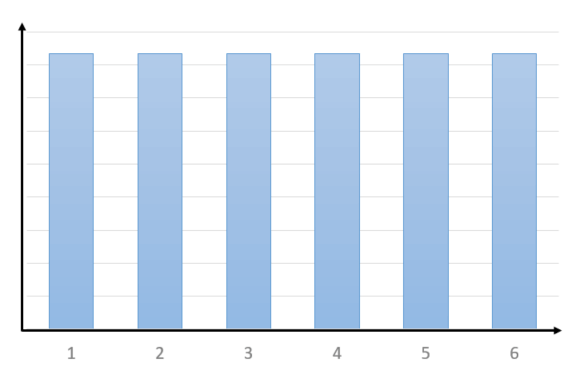
- 主な特徴
-
- 全ての結果は同様に確からしい(等確率)
- 棒の高さは全て同じ
- 期待値に予測力は無い -> 有益な情報を得づらい
- 具体例
-
- サイコロを振った結果
- トランプのカードを引いた結果
- 表記法
-
- \(X \sim U(a,b)\)
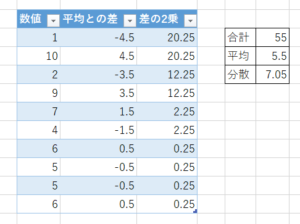
等確率ということは、平均も分散も意味を持たないため、データ活用としての観点では意味を持たない数値という事になり「予測力がない」という事が言えます。

ベルヌーイ分布
\(X \sim Bern(p)\)
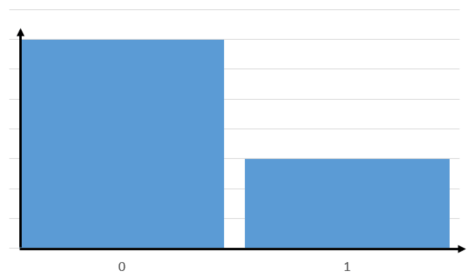
一般的に結果の成功を1と表現し、失敗を0とします。
それぞれの確率は
\(
P(X = 1) = p \\
P(X = 0) = 1-p
\)
- 主な特徴
-
- 試行は一回
- 結果が二種類
- 一方の確率がPとした場合、もう一方は1-Pと表現できる
期待値 \(E(X) = p\) 分散 \(V(X) = p(1-p)\) - 具体例
-
- コイン投げ(表と裏)
- クイズ(YES・NO)
二項分布
\(X \sim B(n,p)\)
\(n\)回のベルヌーイ試行で、\(k\)回成功する確率は
\(
P(X = k) = {}_n C_{k} \times p^k \times (1 – p)^{n-k}
\)
- 主な特徴
-
- n回試行をした場合における確率(0=成功する回数)を求めるもの
確率密度関数 \(
P(X = k) = {}_n C_{k} \times p^k \times (1 – p)^{n-k}
\)期待値 \(E(X) = n \times p\) 分散 \(V(X) = n \times p \times (1-p)\) - 具体例
-
- コインを五回投げた場合に何回表が出るか
- ガチャで0.1%の確率で当たるキャラを10回中、2回当てる確率
- 表記法
-
- \(X \sim B(5, 0.5)\)
- コインを五回投げる(n)、コインが表が出る期待値は0.5(p)
ポアソン分布
予備校のノリで学ぶ「大学の数学・物理」:
【大学数学】ポアソン分布(具体例やその意味、ポアソンの極限定理)【確率統計】
\(X \sim Po(\lambda)\)
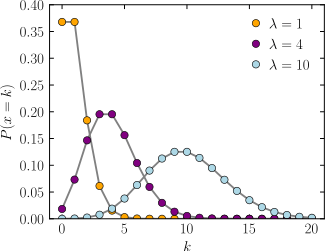
一般的な確率で用いられる変数Pの代わりに、ある期間における発生回数を示した\(\lambda\)が使われます。
特定の期間に平均\(\lambda\)回起こる事象が、ちょうど\(k\)回起こる確率は
\(P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}\)
- \(e\)はオイラー数またはネイピア数と呼ばれています。その値は\(2.71828 \dots\)と続く超越数です。
- ある値の累乗は\(x^{-n} = \frac{1}{x^n}\)と表せられるため、\(e^{-\lambda}= \frac{1}{e^{\lambda}}\)を示します。
- 主な特徴
-
- ある期間に事象が発生する回数を示している
- 分布は常に0から始まる=マイナスの回数の事象は存在しない
- 期待値 = λ
- \( \mu = \sigma^2 = \lambda\)(平均 = 分散 = λ)
- 具体例
-
- 1日のブログのPV数が平均1000PVのサイトが、1日に2000PV見られる確率
連続分布の種類
統計学で区間推定や仮説検定でも良く用いられるのが連続分布でもあります。
連続分布の特徴は
- 標本空間が無限 -> それぞれの値の頻度を求めることはできない
- 表形式でデータを整理することが出来ない -> グラフとして表現 -> グラフの式として表せるものを確率密度関数という
を表します。

| 連続分布の種類 | 特徴 |
|---|---|
| 正規分布 | ベルの形状をしており、実生活でよくみられる分布 |
| スチューデントのT分布 | 標本が少ない場合に見られる正規分布の形 |
| カイ二乗分布 | ・非対称性 ・右に歪んでいる |
| 指数分布 | 数字が急速に変わる場合に見受けられる分布 |
| ロジスティック分布 | 二択の判別をする場合などにおいて使われる分布 |
正規分布
\(X \sim N(\mu, \sigma^2)\)
- 主な特徴
-
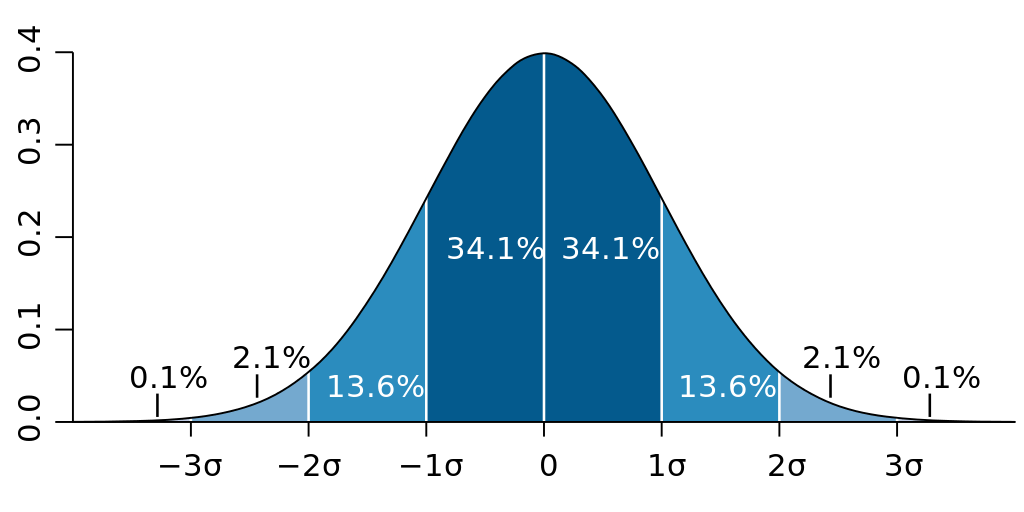
- グラフは鐘の形をしており、左右対称
- グラフの最も高い頂点は最も確率が高い平均となる
- \(\mu \pm \sigma\)で68%のデータが入る
- 具体例
-
- 日本人の体重の値
- 人間が走る速さ
- 表記法
-
- \(X \sim N(\mu,\sigma^2)\)
スチューデントのT分布
\(X \sim t(k)\)
- 主な特徴
-
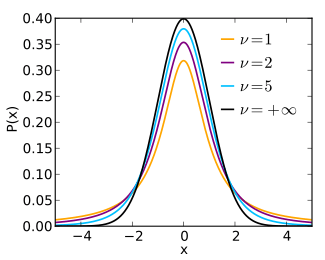
- 少ない標本で、正規分布を近似する
- 正規分布と同様に鐘の形をしており左右対称
- 正規分布と比べて両端が厚く、確率が高くなっている
- 具体例
-
- 標本の数が少なく、正規分布が想定されるときに用いられる
- 表記法
-
- \(X \sim t(k)\)
カイ二乗分布
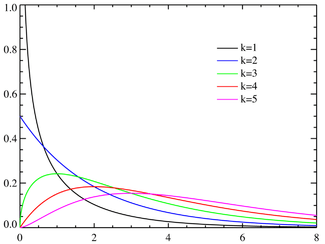
作成中。
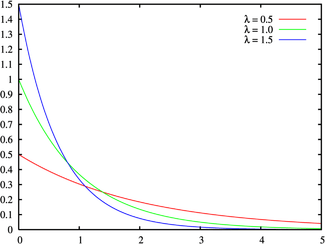
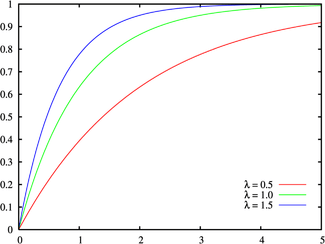
指数分布
- 確率密度関数(PDF)と累積分布関数(CDF)
作成中。
ロジスティック分布
作成中。

コメント