【統計学】記述統計量のまとめ(平均・分散・標準偏差・変動係数・共分散・相関係数)

記述統計での頻出の用語・公式をまとめました。
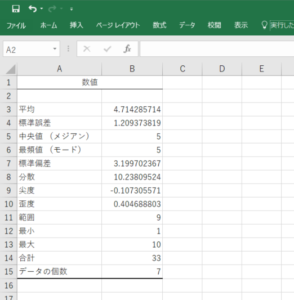
平均(average)
母集団の平均 = \(\mu=\frac{\sum_{i=1}^{N}x_i}{N}\)
標本の平均 = \(\bar{x}=\frac{\sum_{i=1}^{n}x_i}{n}\)
- 説明
-
サンプル数nを合計して、nの数で割ったもの。
- 補足
-
\(\sum_{i=1}^{n}\)は始まりは1からnまでを表し、合計値を\(\frac{1}{n}\)で割るという意味。
- Excel関数
-
AVERAGE(データの範囲)
分散(variance)
分散 = VAR.S(データの範囲)
母分散 = \(\sigma^2=\frac{\sum_{i=1}^{N}(x_i-\mu)^2}{N}\)
標本分散 = \(S^2=\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{n-1}\)
- 母分散は、平均値を引き2乗した合計値をデータ数で割る。
- 標本分散は母分散と計算方法と一緒だが、不偏分散の場合には「データ数-1」で割る。
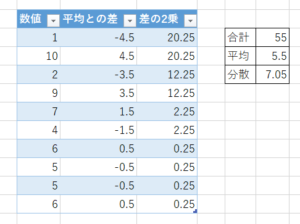
標準偏差(standard deviation, SD, stdev)
標準偏差 = STDEV.S(データの範囲)
分散の値と同様に、データの散らばり度合いを表す。
分散の値を平方根で割った数値です。2乗されて大きくなった数値を戻しています。
母集団の標準偏差 = \(\sigma=\sqrt{\sigma^2}\)
標本の標準偏差 = \(S=\sqrt{S^2}\)
同様のデータのバラつき具合を図る尺度として用いられます。
変動係数(Coefficient of Variation, CV)
変動係数 = STDEV.S(データの範囲) / AVERAGE(データの範囲)
変動係数 = 標準偏差 / 平均値
変動係数は相対標準偏差とも呼ばれています。
対象となるデータが2種類以上ある場合、それらを比較するために用いられます。
異なるデータを標準偏差で比べても意味を持たないため、変動係数が使われます。
共分散(covariance, Cov)
共分散 = COVARIANCE.S(配列)
2種類のデータの関係性を表す指標です。
それぞれのデータごと、平均値を引いた合計値にデータの数で割ったものです。
母集団の共分散 = \({\LARGE\sigma} x y=\frac{\sum_{i=1}^{N}(x_i-\mu_y)*(y_i-\mu_y)}{N}\)
標本の共分散 = \({\large S} x y=\frac{\sum_{i=1}^{n}(x_i-\bar{x})*(y_i-\bar{y})}{n-1}\)
相関係数(correlation coefficient)
相関係数 = CORREL(配列)
2つの値の共分散をそれぞれの標準偏差で割ると求まります。
-1~1の間を値を取り、-1もしくは1の値に近ければ近い程、強い相関関係があると考えられます(正負の相関)。
- Cov:共分散
- Stdev:標準偏差

コメント