【統計学】仮説検定とは？

信頼区間では、母平均がある範囲内にある確率を示すものでしたが、実社会ではある結果が「肯定」なのか「否定」なのか判断しなければならない場合があります。

このような問題を解決する方法として、「検定」という考え方があります。

検定とは

検定(統計的仮説検定)とは、具体的な仮説を立て確率をもとに結論を導く方法です。

検定を実施する目的として「データを元にした意思決定」を行うことが一般的ですが、それは5つのステップで行います。

つまり、「仮説」とは「検定可能な考え方」と言い換えられるでしょう。

帰無仮説と対立仮説

仮説については、具体的に検証できる内容ではなくてはいけません。

また、仮説が正しいか検証する場合、普通はその仮説そのものを検証しますが、統計学のお作法として否定したい仮説を主としておき、主張したい仮説を対立する仮説とします。

例えば、「ある母集団の平均体重は65kgではない」と仮説した場合、帰無仮説と対立仮説は

• 帰無仮説：ある母集団の平均体重は65kgだ
• 対立仮説：ある母集団の平均体重は65kgではない

\(
（帰無仮設）H_0:\mu_0 = 65 \\
（対立仮説）H_1:\mu_0 \neq 65
\)

となり、帰無仮説の整合性を検証します。

標本の平均が、母平均に十分近ければ帰無仮説を採択し、母平均から離れていれば棄却するとします。

• あくまで検定が参照するのは標本ではなく、母集団のパラメータとなるので注意が必要です。

有意水準と棄却域

有意水準とは、仮説が正しかった場合に帰無仮説を棄却する確率。

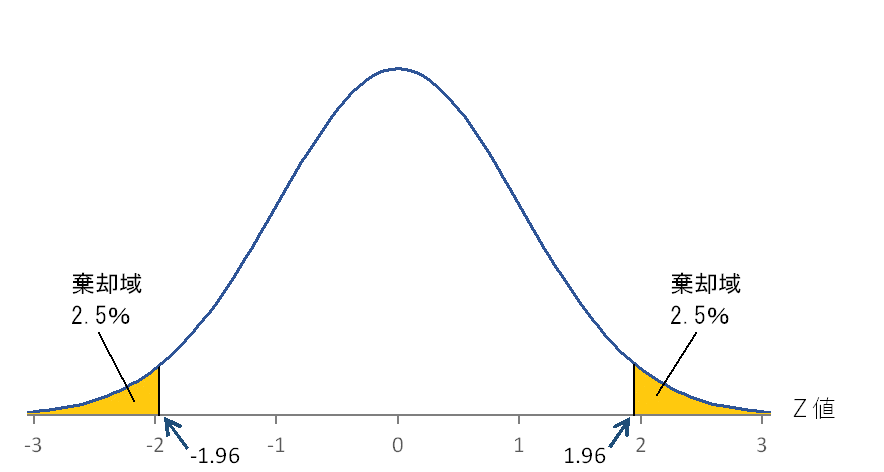
検定では、データから算出された検定統計量より極端な値をとる確率が有意水準と比較して大きいのか、小さいのかに基づいて帰無仮説を棄却するかどうかを判断します。

有意水準5％の棄却域といった表現をします。

両側検定と片側検定

棄却域は対立仮説の内容によって、両側検定か片側検定かが決まります。

例えば、帰無仮説が「母集団の平均体重は65kgだ」とした場合、対立仮説は

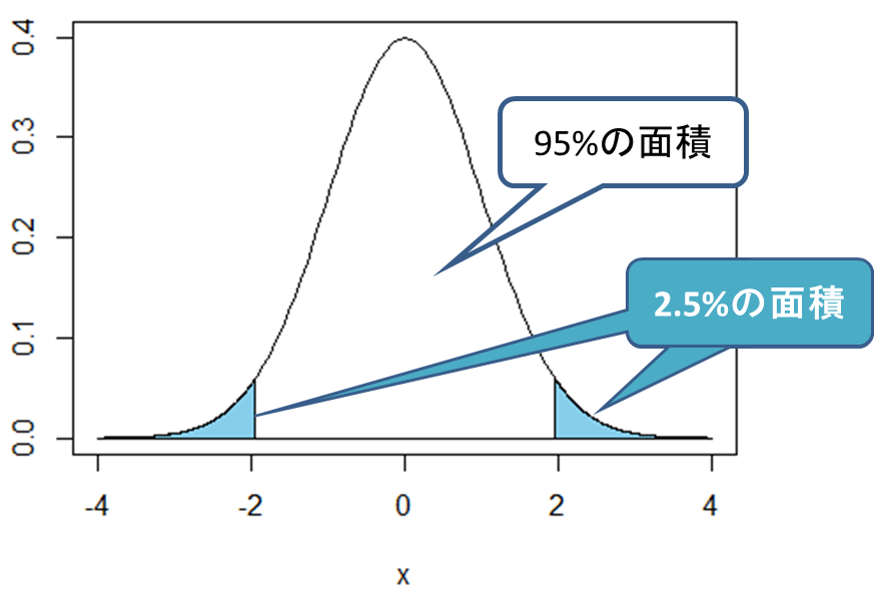
• 母集団の平均体重は65kgではない => 両側検定
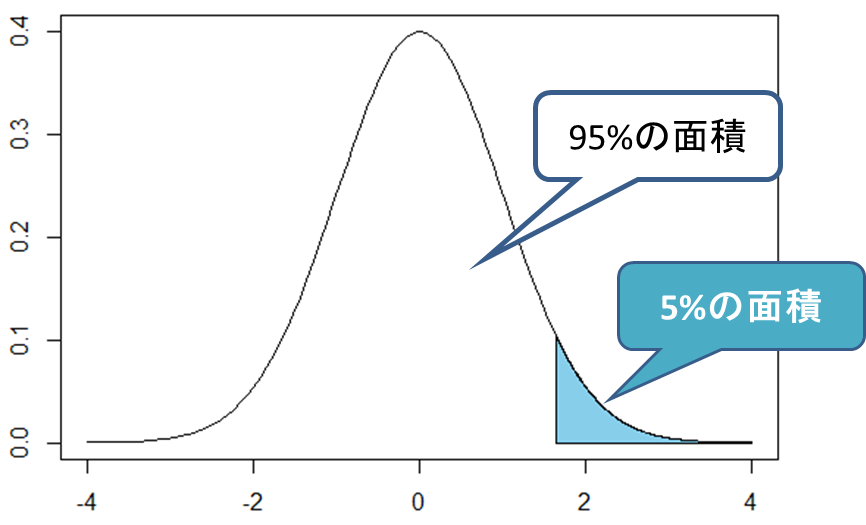
• 母集団の平均体重は65kgより大きい => 片側検定

などが考えられます。

つまり、棄却域の分布が異なるということですね。

両側検定と片側検定では、両側検定のほうが棄却域が狭くなるため、片側検定のほうが棄却されやすくなります。検定を行う前に予めどちらで行うかは決めておく必要があります。

検定結果の流れ

仮説検定を行う手順は以下になります。

1. 帰無仮説を設定する => 母集団の平均体重は65kgだ
2. 対立仮説を設定する => 母集団の平均定住は65kgより高い
3. 帰無仮説が正しいと仮定する
4. 有意水準・棄却域を設定する => 有意水準5％の棄却域
5. 標本から検定統計量を計算する
6. 検定統計量と棄却域を比較する => 検定統計量が棄却域にあるか・ないか
7. 帰無仮説棄却の判断を行う

仮説検定の過誤（第一種の過誤、第二種の過誤）

過誤とは、仮説検定を行った際に間違った判定を行ってしまう事をいいます。

1. 第一種の過誤（誤判定）：帰無仮説が正しくないのに採択してしまう確率
2. 第二種の過誤（検出漏れ）：帰無仮説が正しいのに棄却してしまう確率

の2パターンがあり、正しい結果をそれぞれ得られない。

	\(H_{0}\)は正しい	\(H_{0}\)は間違い
採択	正しい	第2種の過誤 （検出漏れ）
棄却	第1種の過誤 （誤判定）	正しい