【確率】集合(和集合・積集合)から条件付確率・ベイズ理論について

中学・高校で習った集合から、条件付確率・ベイズの定理について記載しています。
集合と事象
集合は、ある値を持つ要素の集まりのこと。どんな事象であっても、結果としての集合が存在します。
事象 ➡ 結果の集合(対象の結果)
集合と要素
ある事象から生まれた結果の集合は
- 全体の「集合」
- 集合の中の一つ一つを「要素」
となります。
変数の場合は「集合」を大文字、「要素」を小文字で表される。
例:\(x \in A \)(xはAの要素である)
表記方法のまとめ
| 表記 | 解釈 | 例 |
|---|---|---|
| \(x \in A\) | 要素xは集合Aの一部 | ネコ \(\in\) 動物 |
| \(A \ni x\) | 集合Aは要素xを含む | 動物 \(\ni\) ネコ |
| \(x \notin A\) | 要素xは集合Aの一部ではない | たんぽぽ \(\notin\) 肉 |
| \(\forall x:\) | ○○のようないかなるxにおいても | \(\forall x:x \in 偶数\) |
| \(A \subseteq B\) | AはBの部分集合 | 偶数 \(\subseteq\) 整数 |
複数の事象
事象Aと事象Bを満たす集合は、3つに分けられます。
- 重複しない
- 一部重複する
- 完全に重複する
重複しない

一部重複する
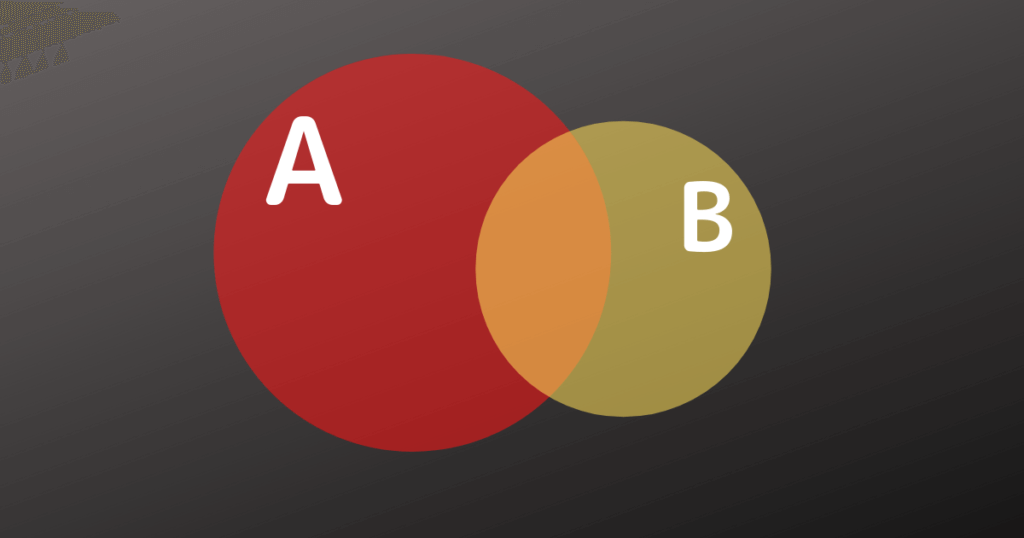
完全に重複する
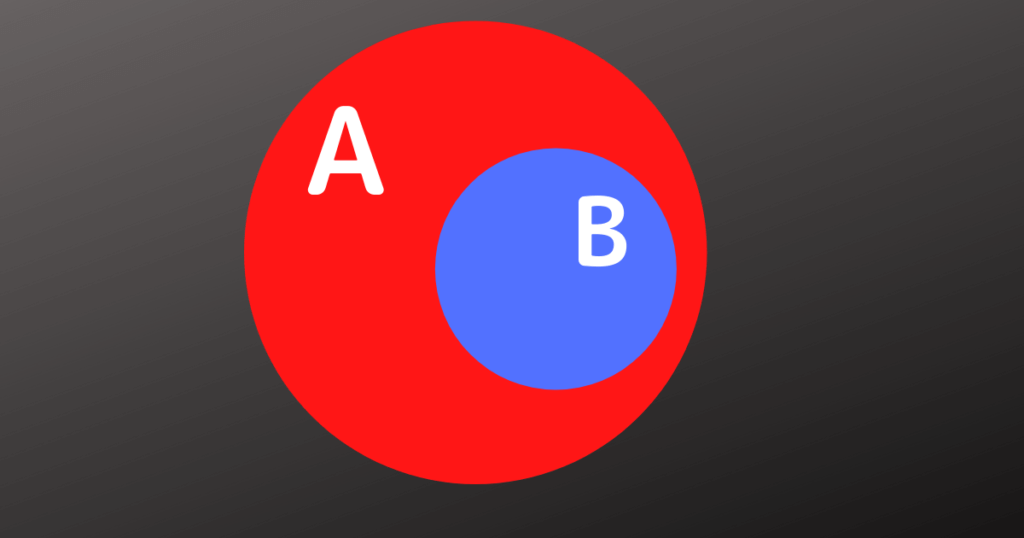
集合の種類
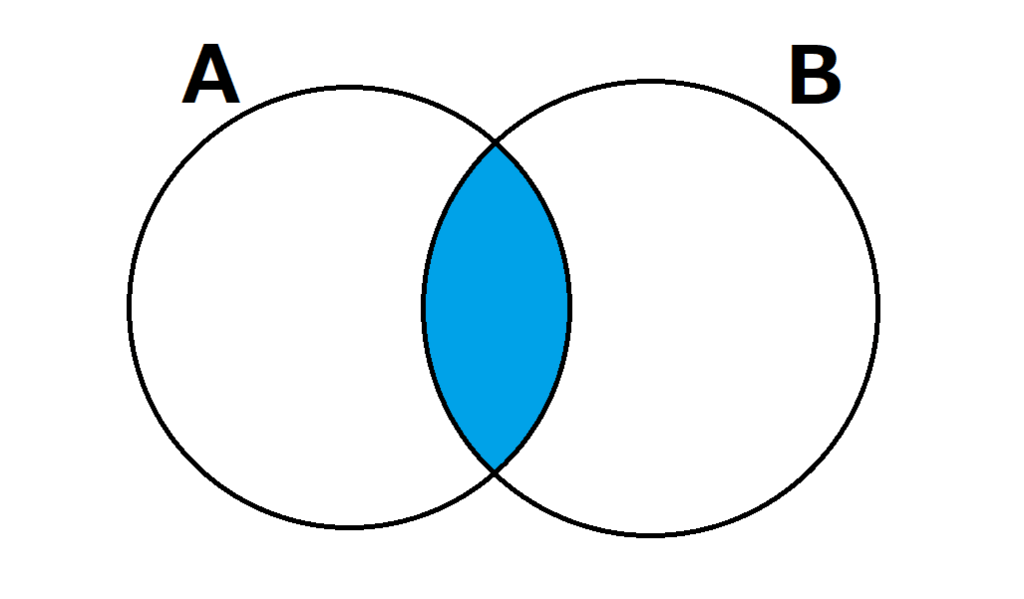
積集合(\(A \cap B\))
2つ以上の事象の重複は、それぞれを同時に満たす集合部分のこと。
\(A \cap B\)
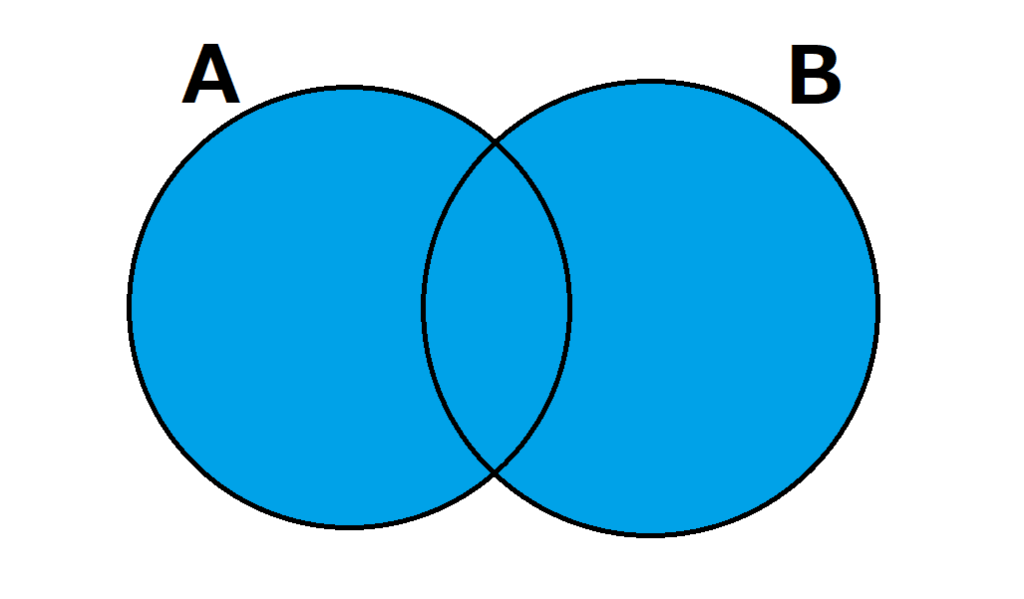
和集合(\(A \cup B\))
AとBの少なくともどちらか一方に属する要素全体の集合をAとBの和集合という。
\(A \cup B\)
すなわち、\(A \cup B = A + B – A \cap B\)となる。
排他集合
\(A \cap B = \emptyset\)ならば、その二つは排他集合となる。
事象の独立と従属
\(P(A)\)が、事象Bの発生で影響を受ける場合はAとBは従属の事象と言えます。
逆に、AとBが従属でない場合はAとBは独立といえます。
Bが発生した場合においてAが発生する確率は、\(P(A|B)\)で表現することが出来ます。これを条件付きの確立といいます。
- 独立
-
- Aが発生する確率は、Bが発生する確率に影響を受けない。
- \(P(A|B) = P(A)\)
- 従属
-
- Aが発生する確率は、Bが発生する確率に影響を受ける。
- \(P(A|B) \neq P(A)\)
条件付き確率
予備校のノリで学ぶ「大学の数学・物理」:【大学数学】ベイズの定理【確率統計】
異なる事象(AとB)が発生したことを想定し、ある事象が起こる確率。
例えば、二つの事象が独立している場合は
\(P(A \cap B) = P(A) \times P(B)\)
となるが、二つの事象が関連性がある(条件付き確率)場合は以下の式になる。
事象Bが起こった確率の下で、Aが起こる確率は
\(P(A | B) = \frac{P(A \cap B)}{P(B)} \)
- P(A | B) = 事象Bが発生した場合の、事象Aの確立
- 条件として\(P(B) > 0\)となります。なぜなら、0という事は事象Bが絶対に発生しないという事になるからです。
二つの事象の従属の関係性を見ると、事象Bが発生した場合だけ対象になります。
つまり条件付き確率は、事象AとBの積集合の範囲とも言えますね。
\(P(A | B) = P(B | A)\)だとしても、AとBの順序が変わると意味が異なる。

ベイズの定理
ベイズの定理は、異なる条件付き確率を計算することで、二つの事象の関係を見るために用いられます。
\(P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\)
P(B)を事象Aが起こる前に分かっている事象Bがおこる確率(事前確率)、P(B|A)を事象Aが起きた後の事象Bがおこる確率(事後確率)となる。

コメント