【統計学】母分散の区間推定

2022-04-102024-03-23

当ページのリンクには広告が含まれています。

母分散を知りたいケースとは？

母分散は、母平均や母比率などと比べて使用用途が少しイメージしづらいかもしれません。

では、母分散ではどのようなケースで活用されるのでしょうか。例えば、

など母平均とは違った視点でデータを見れるようになれますね。

特に、ネジなどの工業製品では精度が命なのでバラツキが生じてしまっては問題ですよね。さらに、平均的には±0だとしても特定のネジが基準値よりも高くても低くても問題ですよね。

このような場合によく用いられます。

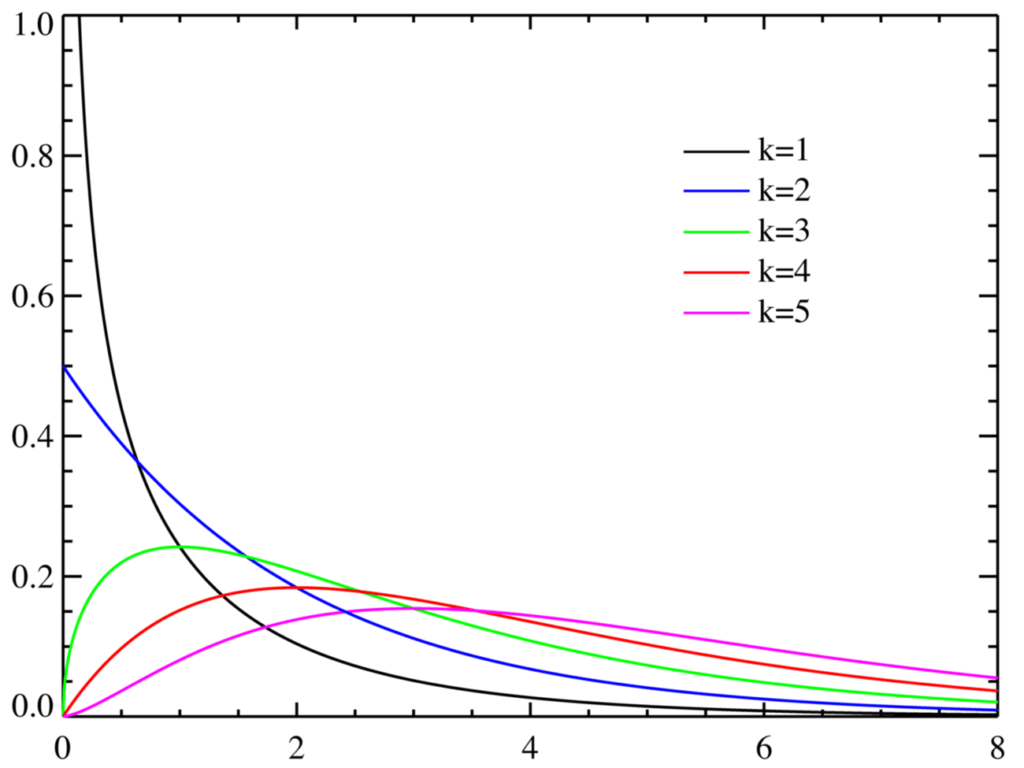
カイ二乗分布は、正規分布に従う確率変数のばらつきがしたがう分布です。図からも分かるように自由度が高くなるにつれ、右にずれていく性質を持ちます。

ある正規分布にしたがう母集団から、n個の標本を抽出して標本平均と不偏分散を得たとして考えてみると、カイ二乗分布は

\(X^2 = \frac{(n-1)*不偏分散}{母分散\sigma^2} \)

母分散の区間推定でも、この考え方を用いて区間推定を行います。

前述した考え方を用いて母分散の区間推定を行います。母分散を\(\sigma^2\)、不偏分散を\(S^2\)とした場合、式は

\(X^2 = \frac{(n-1)S^2}{\sigma^2}\)

となりました。例題で計算してみましょう。

ある工場のネジの寸法誤差の母分散を95％信頼区間で推定したい。
母集団から10個の標本を抽出し、標本平均は0cm、不偏分散は\(0.3^2\)だった。

サンプル数は10個、不偏分散が\(0.3^2\)なので、カイ二乗分布の自由度は10-1で9になります。

今回は両側95％の信頼区間なので下記の表から値を取得します。

これらを式にすると

\( 2.7 \leq \frac{(10-1)0.3^2}{\sigma^2} \leq 19.02 \)

\(0.04 \leq \sigma^2 \leq 0.3\)

つまり標準偏差にすると

\(0.2cm \leq \sigma \leq 0.547cm\)

ということですね！細かい！

よかったらシェアしてね！