【統計学】母比率の区間推定（二値変数とベルヌーイ分布）

二値変数とベルヌーイ分布

二値変数

二値変数とは、コインの表裏・男性と女性のような2つの値をとりうるカテゴリ変数のことを言います。また、表=1、裏=0のように数値として符号化して扱います。

ここで「表が出る比率（確率）」を求めてみます。コインを6回投げたとして

表、表、裏、裏、表、裏

表を1、裏を0として計算すると

\(\frac{1+1+0+0+1+0}{6} = 0.5\)

表が出る比率（期待値=p）は50%となりました。

ベルヌーイ分布

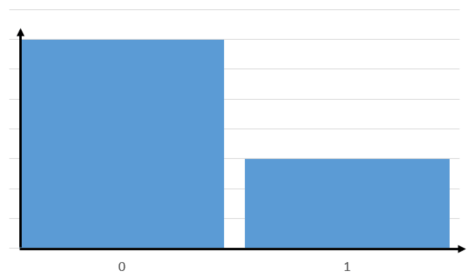
ベルヌーイ分布とは、単一の試行で、結果が二つの場合において構成される分布のことをいいます。

例えば、「コインを投げた結果の全て」を母集団とした場合、いくつかの結果を標本として抽出して考えてみると、これらの二値変数は

• 平均 = \(p\)
• 分散 = \(p(1-p)\)

のベルヌーイ分布にしたがいます。

なぜ分散がp(1-p)で表されるかというと、一方の確率が高い場合には偏りが大きくなるので分散が小さくなります。逆にどちらも等しい場合が最も分散が大きくなります。

さらに、比率=期待値=平均ということになるので「平均の性質」と中心極限定理の考え方を使って

二値変数の比率は標本平均=\(p\)、標本分散=\(p(1-p)/n\)の正規分布にしたがうと考えられます。

この考え方を用いて母比率の区間推定を行います。

母比率の区間推定

母比率をP、標本比率をRと表現すると、母比率の95％信頼区間の公式は以下のように表現されます。

\(P = R \pm 1.96 \times \sqrt{\frac{R(1-R)}{n}}\)

例えば、東京都である施策についての「賛成」か「反対」かを都民からアンケートを取ったとします。

• アンケートに答えてくれた人：200人
• 賛成と答えた人：120人

この場合、都民全体での「賛成」の母比率の95%信頼区間はどうなるのでしょうか。計算してみましょう。

• サンプル数：n = 200
• 賛成と答えた比率 ：平均 = 0.6
• 分散：0.6(1-0.6)/200

サンプル数は十分多く、正規分布に従うので

\(-1.96 \leq \frac{0.6-p}{\sqrt{0.6(1-0.6)/200}} \leq 1.96\)

\(51.7％ \leq \mu \leq 68.3％\)

と計算できました！