【推測統計】頻出の用語・公式まとめ【inferential statistics】

推測統計とは、標本のデータから母集団を予測する際に使われる考え方をいいます。
確率分布(probability distribution)
分布とは、ある事象が起こりえる頻度(確率)を図示したもの。
すなわち、ある結果が起こる確率を分布としてまとめたものが、「確率分布」です。

確率分布の種類
主に「離散分布・連続分布」の二つの種類があり違いとしては結果の数が有限か無限かによって異なります。
有限の場合、それぞれの結果の確率は独立したものになりますが、無限の場合は値を区切ることが出来ないので確率関数として表され、滑らかな曲線を描きます。
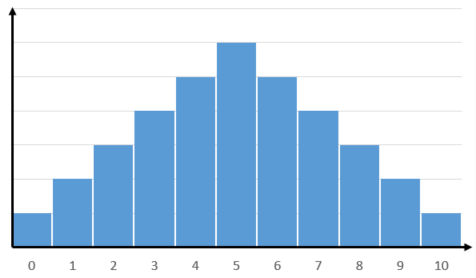
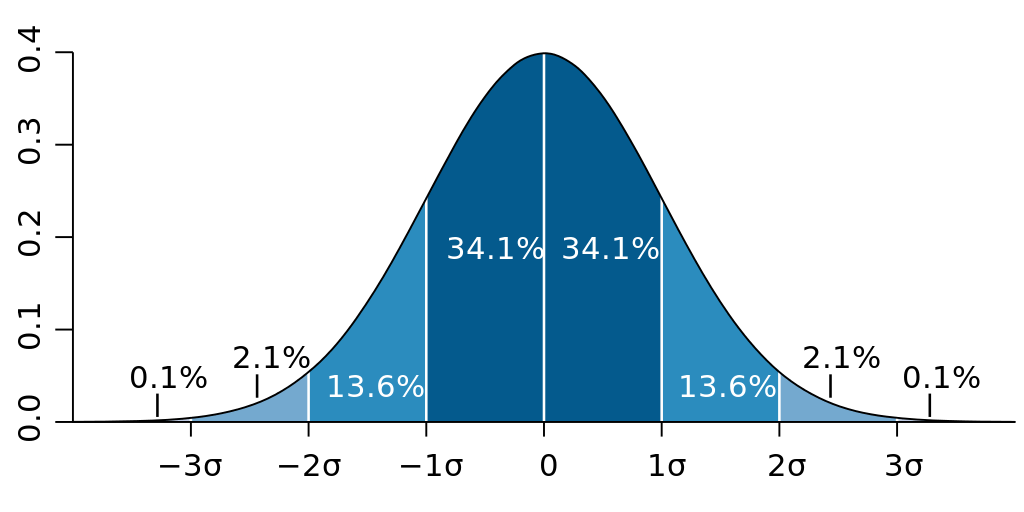
これらの確率分布は信頼区間の区間推定や仮説検定の際に用いられます。

標準化(standardization)
分布のパラメーターである「平均」の値を0、「分散」の値を1にすること。
\(\sim(\mu,\sigma^2)\ \rightarrow\ \sim(0,1)\)
式で表すと\(\frac{x-\mu}{\sigma}\)となります。
中心極限定理(central limit theorem, CLT)
ある母集団から標本を取り、大きい標本平均の分布を作成した場合は「近似的に平均\(\mu\)、分散\(\frac{\sigma^2}{n}\)の正規分布の形に従う」。
標本分布 \(\sim N(\mu,\frac{\sigma^2}{n})\)
中心極限定理を用いることで、母集団がどんな分布であっても正規分布の特徴を活かして分析が可能になる。
標準誤差 (Standard Error, SE)
\(SE = \sqrt{\frac{\hat{\sigma}^2}{n}}\)
- \(\hat{\sigma}^2\) = 不偏分散
- n = サンプルサイズ
標本平均にて作られた「標準偏差」のこと。
母集団との平均値の差異を定量的に示せるため重要な値となる。

信頼区間(Confidence interval, CI)
信頼区間とは、母平均や母分散がある確率の中で、存在する範囲を示したもの。
信頼区間の求めるには、標本のデータを用います。
点推定( point estimation)
点推定は、単一の数字を示す。
信頼区間の中心(点推定)=平均値を表す。
母平均の区間推定
母集団が正規分布であることを前提に考え、正規分布でなかったとしても「中心極限定理」を活用し正規分布であると考えられます。
標本が1つの母平均を求める場合には2パターンあります。
- 母分散が既知の場合
- 母分散が未知の場合
それぞれ計算方法が若干異なるので、注意が必要です。
また基本的には、実社会では母分散が未知の場合がほとんどであるため、①はほとんど使えません。
①母分散が既知の場合の信頼区間
予備校のノリで学ぶ「大学の数学・物理」:推定・検定入門③(区間推定:分散が既知な場合)
\(\mu = \bar{X}\pm{Za/2}\frac{\sigma}{\sqrt{n}}\)
\(\bar{x}\)が標本平均=点推定となり、\(\frac{\sigma}{\sqrt{n}}\)は標準誤差となります。
αの値は「信頼度」によって異なり、信頼度95%の場合
α = 1-0.95 = 0.05,これをα/2で0.025となり
標準正規分布表から\(Z_{0.025}=1.96\)となります。
つまり、\(
\bar{X}-1.96\frac{\sigma}{\sqrt{n}}
\leq \mu \leq
\bar{X}+1.96\frac{\sigma}{\sqrt{n}}
\)となります。
②母分散が未知の場合の信頼区間
予備校のノリで学ぶ「大学の数学・物理」:推定・検定入門④(区間推定:分散が未知な場合)
\(\mu = \bar{X}\pm{t_{n-1}},a/2\frac{U}{\sqrt{n}}\)
母分散が分かっている場合との違いは
- Z値(正規分布)ではなくT値(スチューデントのT分布)を用いる
- 母分散が分からないので、不偏分散を用いる(\(U^2\))
このようにして計算を行います。
特徴として、母分散が既知の場合と比べデータの不確実性が高くなり信頼区間の幅も広くなります。
母比率の区間推定
予備校のノリで学ぶ「大学の数学・物理」:推定・検定入門⑥(母比率の推定)
\(P = R \pm{Za/2}\sqrt{\frac{R(1-R)}{n}}\)
比率とは、母集団での「YES・NO」のような分類できるようなもの。
- 母比率:\(P\)
- 標本比率:\(R\)
で表現され、前提としてnが十分大きい必要がある。
母比率の95%信頼区間を推定する場合には
\(R – 1.96\sqrt{\frac{R(1-R)}{n}} \leq P \leq R + 1.96\sqrt{\frac{R(1-R)}{n}}\)となる。

母分散の推定
予備校のノリで学ぶ「大学の数学・物理」:推定・検定入門⑦(母分散の推定)
- 正規分布を条件
- \(x^2\)分布を用いる
\(
下限値 = \frac{(n-1)U^2}{x^2(n-1,a/2)} \
上限値 = \frac{(n-1)U^2}{x^2(n-1,1-a/2)}
\)
許容誤差(Margin of Error, ME)
許容誤差は、信頼区間での範囲といえます。
信頼区間\(
= \bar{x}(標本平均) \pm{ME}(許容誤差)
\)
といえます。つまり、許容誤差の求め方は
母分散が
既知の場合の許容誤差 = \(Za/2\frac{\sigma}{\sqrt{n}}\)
未知の場合の許容誤差 = \(t_{n-1},a/2\frac{S}{\sqrt{n}}\)
となります。
許容誤差が大きいという事は信頼区間が広く、
許容誤差が小さいという事は信頼区間が狭いという事です。
仮説検定
予備校のノリで学ぶ「大学の数学・物理」:推定・検定入門⑧(母平均の検定)
信頼区間では、母平均がある範囲内にある確率を示すものでしたが、実社会ではある結果が「肯定」なのか「否定」なのか判断しなければならない場合があります。
このような問題を解決する方法として、「検定」という考え方があります。
検定を実施する目的として「データを元にした意思決定」を行うことが一般的ですが、それは4つのステップで行います。
- 仮説を立てる
- 適切な検証方法を選定
- 検証を実施する
- 意思決定を行う
つまり、「仮説」とは「検定可能な考え方」と言い換えられるでしょう。
帰無仮説と対立仮説
仮説については、具体的に検証できる内容ではなくてはいけません。
例えば、「自営業者は会社員よりも年収が高い」といった仮説は検証することが出来ません。
一方で、「会社員は自営業者よりも年収が100万円以上高い」といったような具体的な数値を用いた場合には検証できる内容ですので「仮説」になりえます。
帰無仮説とは、「実際に検証を行う仮説」のことです。
一方で、対立仮説とは「帰無仮説以外」を意味します。
例えば、「サラリーマンの給与が550万円である」と帰無仮説を行った場合、対立仮説は「550万円ではない」という事です。
\(
(帰無仮設)H_0:\mu_0 = 550,000 \\
(対立仮説)H_1:\mu_0 \neq 550,000
\)
標本の平均が、母平均に十分近ければ帰無仮説を採択し、母平均から離れていれば棄却するとします。
- あくまで検定が参照するのは標本ではなく、母集団のパラメータとなるので注意が必要です。
有意水準
有意水準とは、仮説が正しかった場合に帰無仮説を棄却する確率。
優位水準はαで表し、一般的には
- 0.01
- 0.05
- 0.1
といった値が用いられます。これは検定においてどの程度の精度を担保するかによって異なります。
生産工場など精密機器:0.01
人の行動など不確定要素が含まれる:0.1
Z検定
\(
Z = \frac{\bar{x} – \mu}{s/\sqrt{n}}
\)
Zスコアは、標本平均を仮説の平均で引いたものを、標準誤差で割ることで求められます。
仮説検定の過誤
過誤とは、仮説検定を行った際に間違った判定を行ってしまう事。
- 第一種の過誤(誤判定)
- 第二種の過誤(検出漏れ)
の2パターンがあり、正しい結果をそれぞれ得られない。
| \(H_{0}\)は正しい | \(H_{0}\)は間違い | |
|---|---|---|
| 採択 | 正しい | 第2種の過誤 (検出漏れ) |
| 棄却 | 第1種の過誤 (誤判定) | 正しい |

コメント