変数間の相関関係の確認と可視化方法【pandas・seaborn】

データ分析を行う際に、「説明変数」との関係性を確認する方法として変数間の相関関係を確認する方法があります。
相関関係とは、一方の値が変化した時にもう一方の値も応じて変化するような関係性を言います。
今回は相関関係を確認する指標の「相関係数」の求め方と可視化方法をご紹介します。
サンプルデータの準備
import pandas as pd
from pandas import DataFrame
from sklearn.datasets import load_irisモジュールをインポートし
iris_target = DataFrame(iris.target,columns=['target_names'])
iris_df = DataFrame(iris.data,
columns=[
'sepal length (cm)',
'sepal width (cm)',
'petal length (cm)',
'petal width (cm)'
])
iris_df = pd.concat([iris_df, iris_target], axis=1)
target_names = {0:'setosa',1:'versicolor',2:'virginica'}
iris_df['target_names'] = iris_df['target_names'].map(target_names)
iris_df.head()| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | target_names | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
上記データを用意しました。
データはアヤメの品種と花の各種幅・長さを示しています。
相関係数とは
「相関係数」とは、相関関係の強さを示す指標です。
相関関係の値が1に近いほど相関が強く、0に近いほど相関(無相関)が弱いと言えます。
例えば、予測モデルを作成する場合に説明変数の選択指針として活用できます。
目的変数と相関が弱い場合には除外したり、相関が強すぎる場合には片方を除外したりします。
相関係数の求め方—corr()
相関係数はpandasのDataFrame.corr()で求めます。
iris_df.corr()| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| sepal length (cm) | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal width (cm) | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal length (cm) | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal width (cm) | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
数値からpetal lengthとpetal widthが強い相関関係があることが分かりました。
相関関係の可視化方法
相関係数だけでは分かりづらいので、グラフで可視化してみます。
- ヒートマップ
- 散布図
- 箱ひげ図
これらを見ていきます。

モジュールのインポート
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline各種必要なモジュールをインポートします。
ヒートマップ—sns.heatmap()
説明変数間の関連性を可視化する場合にはseaborn.heatmap()関数を使います。
sns.heatmap(iris_data.corr())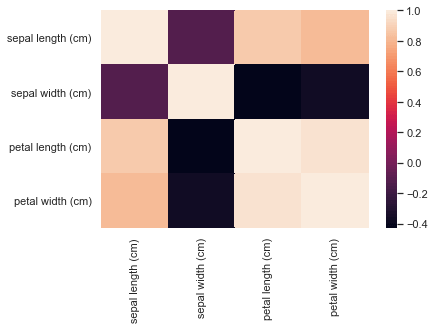
数値を表示—annot=True
マスの中に数値を表示させる場合には引数にannot=Trueとします。
sns.heatmap(iris_data.corr(), annot=True)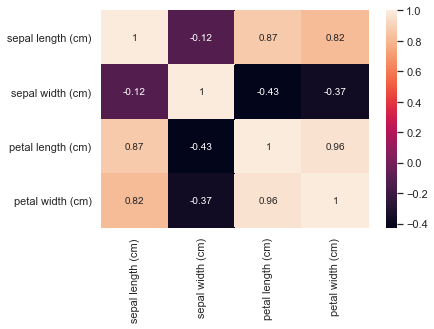
petal widthとpetal lengthで相関係数が0.96と高い相関が出ています。
正方形で表示—square=True
ヒートマップを正方形で表示する場合にはsquare=Trueにします。
sns.heatmap(iris_data.corr(), annot=True, square=True)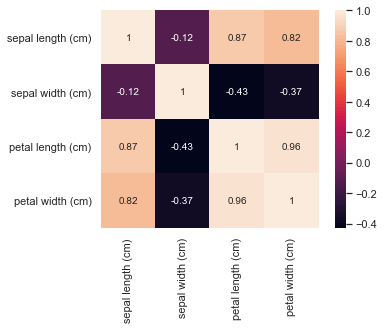
散布図—sns.scatterplot()
2つの説明変数を詳細に分析する場合には、散布図のsns.scatterplot()関数を使います。
引数にはxとy、データを指定します。
今回は、相関係数が高かったpetal widthとpetal lengthを見てみます。
sns.scatterplot(x='petal width (cm)',y='petal length (cm)',data=iris_df)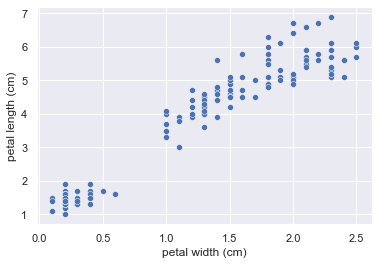
値が大きくなるにつれて、右上に値が変化しています。
これを「正の相関関係」があると言えます。
一方で相関関係が低い場合はどうなるのでしょうか。
相関係数が-0.12だったsepal widthとsepal lengthで作成してみましょう。
sns.scatterplot(x='sepal width (cm)',y='sepal length (cm)',data=iris_df)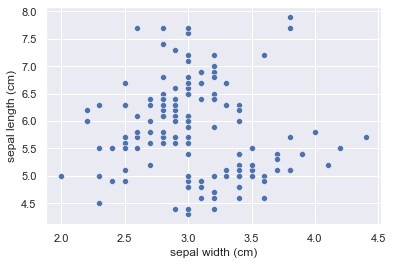
ばらつきが大きく、相関関係は無さそうですね。
箱ひげ図—sns.boxplot()
ヒートマップ・散布図では数値「量的データ」から見たグラフでした。
カテゴリ分類など「質的データ」と比較する場合には箱ひげ図がお勧めです。
箱ひげ図はsns.boxplot()関数で作成します。
アヤメの品種と長さを見てみましょう。
sns.boxplot(x='target_names',y='petal length (cm)',data=iris_df)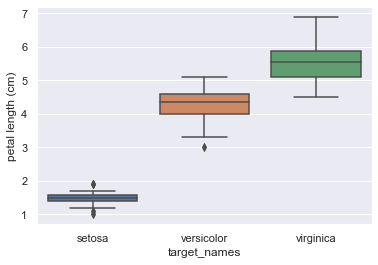
sns.boxplot(x='target_names',y='sepal width (cm)',data=iris_df)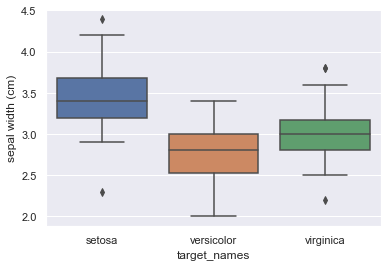
- 菱形マーク—外れ値
- 上下の横棒バー—最大値・最小値
- 真ん中—四分位範囲(全体の50%)
を示しています。
品種によってばらつきが生じているので相関関係があると判断できそうです。
参考
pandas公式ドキュメント:pandas.DataFrame.corr
seaborn公式ドキュメント:seaborn.heatmap
機械学習・データ処理を学ぶのにおすすめの教材
じっくり書籍で学習するなら!





コメント