微分・積分の公式の計算

微分の計算
https://sci-pursuit.com/math/differential-1.html
\( x^n \)の微分公式
\( y = x^2 \rightarrow f^{\prime}(x) = nx^{n-1} \)
\( nx^{n-1} \)の微分公式
\( y = kx^n \rightarrow f^{\prime}(x) = k × nx^{n-1} \)例題
\( y = -x^3 \)
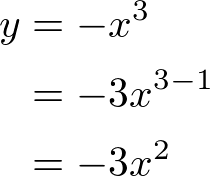
\( y = 7x + 10x^2 \)
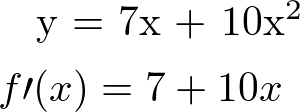
\( y = 3x^2 – 6x + 3 \)
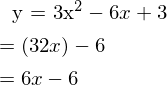
積分の計算
積分とは微分と対を成すもので、ある関数から得られる領域の面積を求めることです。
積分では「 \( \int \) (インテグラル)」という記号を使います。例えば次の式は、「\( f(x) \) という関数を\(a\)から\(b\)まで積分する」ということを表します。
\( \int_{b}^{a} f(x)dx \)
これは、\( x = a, x = b, y = f(x), \)軸( \( y = 0 \) )の4本の線で囲まれる部分の面積(次の図の網掛け部分)を計算することを意味します。
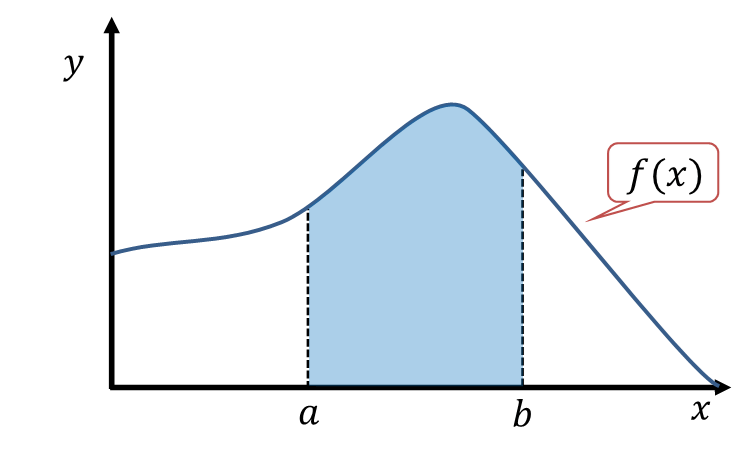
この\( f(x) \)関数を使って、積分の考え方を説明します。
\( \int_{a}^{b} f(x)dx \)
ある関数\( f(x) \)を積分する際に、\( a \leq x \leq b \)といった具体的な区間が与えられた場合には、
\( \frac{d}{dx}F(x) = f(x) \)
という関係となる\( F(x) \)を用いて\( F(b) – F(a) \)と引き算することで答えを算出できます。
\( \int_{a}^{b} f(x)dx = [F(x)]_{a}^{b} = F(b) – F(a) \)
次に、\( F(x) \)このを求めるための公式を紹介します。
\( x^n \)の積分公式
\( x^n \)の形で表される関数の積分は、次のように計算する。
\( \int_{a}^{b} x^ndx = \left[ \frac{1}{n+1}x^{n+1} \right]_{a}^{b} \)
\( \int_{0}^{3}x^2dx = \left[ \frac{1}{3}x^3 \right]_{0}^{3} = \left( \frac{1}{3}×3^3 \right) – \left( \frac{1}{3} × 0^3 \right) = 9 \)
\( kx^n \) の積分公式
\(‘ y=10f(x) \)のような、ある関数\( f(x) \)を定数倍した関数の積分は次の様に計算できます。
\( \int_{0}^{3} x^2f(x)dx = k × \int_{0}^{3}f(x)dx \)
例えば、\( y=x^2+x \)の関数の積分計算は、\( x^2 \)の項と\( x \)の項をそれぞれ積分したものを足し合わせたものと等しくなります。この関数を1から3まで積分すると以下のようになります。
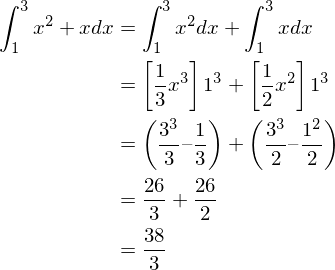
例題
\( \int_{1}^{3} 4xdx \)
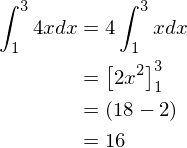
\( \int_{10}^{11}2x+3x^2dx \)
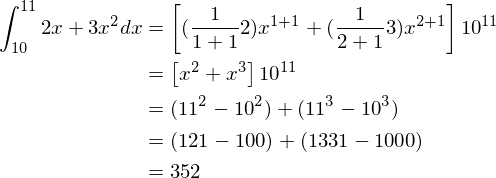

コメント