【確率分布】二項分布を使って試行での成功する確立を求める【例題】

二項分布において「n回のベルヌーイ試行で、k回成功する確率」は下記のように求めます。

\(P(X=k) = {}_n C_{k} \times p^k \times (1-p)^{n-k}\)

今回はこの式を使って、何個か例題を解いてみます。

例題問題の計算

例題①

当たり確率1%のガチャのキャラを当てるために100連ガチャで回します。当たる回数1回の確率は何％ですか？

\(
試行回数： n = 100 \\
当たる回数：X = 1 \\
当たる確率：p = 0.01
\)

で計算すると

\(
\begin{eqnarray*}
P(X = 1) &=& {}_{100} C_{1} \times (1-0.01)^{100-1} \\
&=& \frac{100!}{(100-1)! \times 1} \times 0.99^{99} \\
&=& 0.3697
\end{eqnarray*}
\)

となります。つまり、36.9％の確率で1回当たるという事です。

\({}_n C_{k}の組み合わせの部分は下記記事を参照ください。\)
【確率】階乗・順列・組み合わせについて【組み合わせ論】

例題②

例題①の当たる回数0・2・3回の当たる確率をそれぞれ求め、確率分布を書きなさい。

P(X = 1) = 36.9%でしたので、残りを計算していきます。

\(\begin{eqnarray*}
P(X = 0) &=& {}_{100} C_{0} \times 0.1^0 \times (1-0.01)^{100-0} \\
&=& 0.366
\end{eqnarray*}\) \(\begin{eqnarray*}
P(X = 2) &=& {}_{100} C_{2} \times 0.1^2 \times (1-0.01)^{100-2} \\
&=& 0.184
\end{eqnarray*}\) \(\begin{eqnarray*}
P(X = 3) &=& {}_{100} C_{3} \times 0.1^3 \times (1-0.01)^{100-3} \\
&=& 0.06
\end{eqnarray*}\)

これらの値を使って確率分布を作成します。

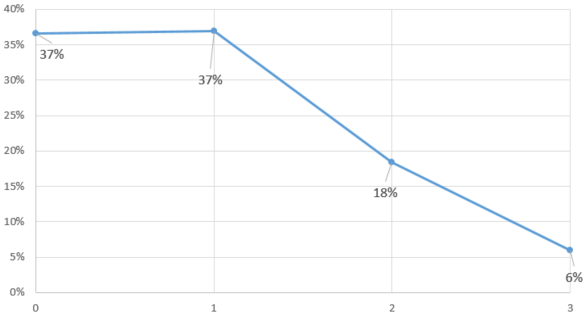
パズドラ世代なのでよくガチャ回してましたが、100回やっても出ない確率が37％もあるのが驚きでした。

もうガチャとか回さん・・・。