【機械学習】線形回帰モデルの特徴と作成・検証【sklearn】

線形回帰モデルとは、予測する値（目的変数）と判断材料となる値（説明変数）との関係性を直線で表現したモデルです。

例えば、予測したい値が「家賃」だとしたら、判断材料は「駅からの近さや広さ」などが説明変数の候補として挙げられます。

この記事では線形回帰の特徴と作成・検証方法についてご紹介いたします。

この記事のサンプルコード

線形回帰の種類

線形回帰には

この2種類があります。計算式にすると単回帰分析の場合は

y = ax+b

になります。中学校に習った一次関数ですね。
一方で重回帰分析の場合は

y = a₁x₁ + a₂x₂ + a₃x₃ … + b

目的変数の数の分だけ増えていきます。
それぞれの説明変数に対して関連性（重み）を計算して直線としています。

線形回帰の特徴

線形回帰の特徴は、計算式がシンプルで人間が解釈しやすいことです。

例えば、重回帰モデルを作成した場合に、説明変数の値の増減の影響を簡単に把握できます。

y(家賃) = 6.9x₂(駅近/M) + 4.5x₂(広さ/㎡) + 8.9

このように表現され、広さが1㎡増えると数値がいくつ増えるのかと理解できます。

自走できるAI人材になるための6ヶ月長期コース【キカガク】

（日本ディープラーニング協会）E資格認定講座！ これまでの受講者数30,000人以上！ ・AI人材となり市場価値を高めたい方へ！

詳しくみる無料カウンセリング予約

線形回帰モデルの作成方法

サンプルデータの準備

sklearnからサンプルデータを用意しました。ボストンの家賃価格です。

import pandas as pd
from pandas import DataFrame, Series
from sklearn.datasets import load_boston
iris = load_boston()
boston_columns = boston.feature_names
X = pd.DataFrame(boston.data, columns=boston_columns)
y = pd.DataFrame(boston.target, columns=['price'])
boston_df = pd.concat([X,y], axis=1)
boston_df.head()

モジュールのインポート—LinearRegression

from sklearn.linear_model import LinearRegression as LR

sklearn.linear_modelからLinearRegressionをインポートします。
長いのでLRとします。

インスタンスを呼び出しておきます。

lr = LR()

モデルの学習方法—fit()

モデルを学習させるには、説明変数=Xと目的変数=yを用意し、lr.fit(X,y)とします。

予測が正しかったかどうか確認するために、データを「訓練用」と「テスト用」に分割します。分割方法はsklearnのtrain_test_split()関数を用います。

あわせて読みたい

【機械学習】sklearnで訓練用・テスト用データで分割する方法 機械学習を行う際には「訓練用データ」と「テスト用データ」の2種類を用意する必要があります。 なぜなら、モデル作成後の精度の確認などモデルの評価を行う必要がある…

X = boston_df.drop('price', axis=1)
y = boston_df['price']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=20)

家賃を予測したいのでpriceを目的変数に、それ以外を説明変数とします。

lr.fit(X_train, y_train)

これで学習できました。簡単ですね。

学習したモデルの使い方—predict()

学習したモデルを使って、予測を行う場合にはpredict()関数を使います。
引数に先ほどと同様に説明変数であるXを渡すと予測値であるyが返ってきます。

テスト用データのX_testを渡してみます。

predict = lr.predict(X_test)
predict

array([21.16529225, 26.98122565, 20.13238425, 23.77739816, 13.52933517,
       19.78781367, 17.21904896,  8.17083014, 18.97336579, 24.92643113,
       27.31648822, 16.56095912, 23.75393667, 22.07802703, 20.0720829 ,
       24.45285089, 31.14247284, 19.56161838, 14.7339778 , 17.70428623,
       38.38674348, 42.19652498, 27.23491992, 32.32243064, 25.61260041,
       26.32051289, 19.91815339, 25.06871068, 21.56340122, 23.56190758,
       20.95737493, 16.97344579, 22.67777514, 11.02937371, 30.07700301,
       20.40885338, 43.41589347, 22.31782684, 19.47047936, 31.37844715,
        7.35315484, 17.02572539, 18.56228142, 12.40449459, 23.27428193,
       28.60405594, 21.40018108, 20.32172238,  9.62621954, 14.44273682,
       35.45001989, 34.36879657, 11.73421146, 36.7666021 , 20.21108332,
       22.13254012, 20.2999414 , 18.66486633, 18.93973142, 22.58399613,
       27.25677358, 20.31699096, 19.81940653, 23.62245173, 17.83581498,
       19.30320011, 27.54553579, 26.34576727, 18.35682807, 18.36012099,
       34.20477474, 17.7141991 , 25.49840291, 22.87070575, 20.68237912,
       25.20766786, 24.05655396, 27.8424379 , 28.66907635, 16.67343161,
        9.23533211, 15.03021663, 23.00209324,  7.91549776, 28.29959409,
       24.78714417, 23.82446999, 18.13446691, 24.50574566, 26.8173704 ,
       23.86239076, 25.6874264 , 18.54611777, 12.85325568, 22.40860954,
       27.41637358, 19.68056608, 19.58360154, 17.48978589, 18.39798043,
       17.87212821, 25.99796821, 20.42151036, 38.43768426, 28.45350548,
       12.69534206, 16.84532487, 14.95637303, 16.05908897, 21.82069474,
       24.39770475, 32.1205306 , 20.58470258, 14.10651906, 28.90912648,
       33.92982917, 27.39056365, 20.96653101, 13.06681601, 24.30456683,
       34.17689664, 14.14254524,  9.58953153, 40.11004131, 23.65382644,
       18.09372281, 21.73536739, 43.31581816, 30.91641637, 21.26831527,
       15.85401686, 25.23367207, 17.61368865, 19.69243984, 32.84494909,
       34.51585071, 24.37545482, 24.98279708, 19.13136221, 26.86948734,
       22.75326174, 20.04619872, 24.32375569, 23.44865889, 12.91033781,
       28.95975157, 20.58555183, 21.97142418,  9.18319728, 21.01741664,
       23.48053115, 16.71138062])

予測値がリストで返ってきました。

説明変数の係数（偏回帰係数）の確認方法

前述したとおり、重回帰分析ではそれぞれ説明変数に重み（係数）をつけて直線を描いているとご説明しました。これを偏回帰係数(傾き)といいます。

それぞれの偏回帰係数を確認してみます。
偏回帰係数はlr.coef_に格納されています。

coef_df = pd.DataFrame(lr.coef_,X_train.columns)
coef_df

各項目の偏回帰係数が求まりました。
切片を求める場合にはlr.intercept_とします。

>>> lr.intercept_
28.687850966054768

学習モデルの評価関数での検証

モデル作成の際には、作成したモデルがきちんと予測できているか検証する必要があります。

まずは予測した数値と本当の数値がどれくらい違いがあるのか見てみます。
検証方法は複数ありますが、今回はRMSEとR²を使ったモデルの精度検証を行います。

あわせて読みたい

【MAE・RMSE・MAPE・R²】線形回帰モデルの評価関数の種類と計算方法 機械学習における評価関数とは「モデルの性能を定量的に評価するための関数」です。 作成するモデルによって使われる評価関数の種類は異なります。 今回は線形回帰モデ…

# RMSEの計算
>>> from sklearn.metrics import mean_squared_error as MSE
>>> import numpy as np
>>> rmse = np.sqrt(MSE(y_test, predict))
>>> rmse
5.039166613497879

RMSEの値は5.039となりました。R²はどうでしょうか。

# R²の計算
>>> from sklearn.metrics import r2_score
>>> r2 = r2_score(y_test, predict)
>>> r2
0.7023964981707973

R²の割合は0.702となりました。つまり70％の精度があると判断されます。
もう少し精度上げたいですね。

通常はくりかえし説明変数の調整→モデル作成→検証を行い、精度を上げていきます。

オンラインAIプログラミングスクール Aidemy Premium

アイデミープレミアムプランで3ヶ月でAIエンジニア！

詳しくみるオンライン相談会

予測精度の可視化

評価関数での評価だけではなく可視化して状況を確認するのもおすすめです。

y_max = np.max(y_test)
y_min = np.min(y_test)
plt.xlabel('Measured Price')
plt.ylabel('Predict Price')
plt.plot([y_min,y_max],[y_min,y_max],'k')
sns.scatterplot(x=y_test, y=predict)

X軸が実測値、Y軸が予測値になります。また、黒い線が基準線です。
散布図の点が黒い線に近ければ近いほど予測が正しいことを示しています。

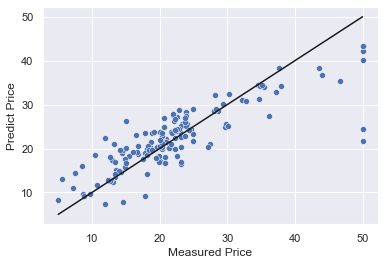
うーん何とも言えないですね・・・。
基準線を水平にする場合は

plt.scatter(y_test, (y_test-predict), c='b', alpha=0.5)
plt.hlines(y=0, xmin=0, xmax=50, colors='black')
plt.xlabel('Price')
plt.ylabel('Price difference')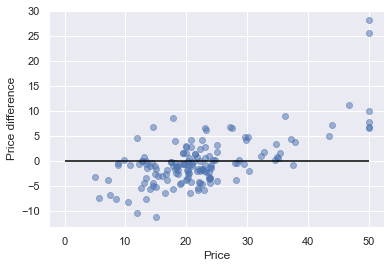

このようになります。
これを「残差プロット」といい、X軸が実際の価格、Y軸が価格差（回帰残差）となります。

Priceが10～40まではまとまっていますが、それ以外については大きくブレが発生していることが分かりました。

参考

この記事のサンプルコード

機械学習・データ処理を学ぶのにおすすめの教材

じっくり書籍で学習するなら！

Python実践データ分析100本ノック

¥318 （2024/11/08 18:48時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ

Python 実践データ加工/可視化 100本ノック

¥830 （2024/11/11 16:04時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ

Kaggleで勝つデータ分析の技術

¥3,608 （2024/11/10 16:43時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ

Pythonデータ分析／機械学習のための基本コーディング！ pandasライブラリ活用入門 impress top gearシリーズ

¥2,090 （2022/02/20 08:45時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ