【MAE・RMSE・MAPE・R²】線形回帰モデルの評価関数の種類と計算方法

機械学習における評価関数とは「モデルの性能を定量的に評価するための関数」です。

作成するモデルによって使われる評価関数の種類は異なります。

今回は線形回帰モデルで頻出の関数の種類と計算方法をご紹介します。

この記事のサンプルコード

線形回帰モデルの評価関数の種類と特徴

線形回帰モデルの特徴は、売上や費用など連続した「数値」を予測するモデルとなります。

つまり、実測値と予測値のズレを評価する必要があります。

このズレを評価する関数として

の4種類がよく使われます。

それぞれ見ていきます。

誤差を測る評価関数—MAE・RMSE

MAE（Mean Absolute Error）

実測値と予測値の「誤差の絶対値」から算出する指標です。
「平均絶対誤差」と呼ばれ、予測精度は0に近いほど高いと言えます。

MAEの計算式

計算式は全データの「実測値-予測値」の平均です。

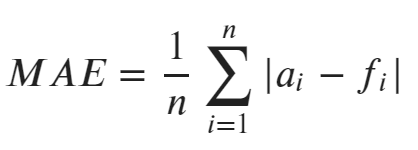
MAEの計算例

実際の数値で考えてみましょう。データを用意しました。

絶対値の値を平均してみます。
データをMAEの数式にすると下記のようになり、MAE=3となりました。

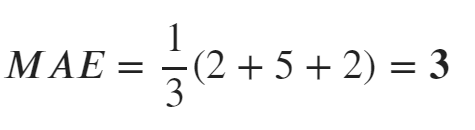
sklearnを使ったMAEの求め方

sklearnにはMAEを簡単に求められる関数が用意されています。

sklearn.metricsからmean_absolute_errorをインポートし
mean_absolute_error(実測値, 予測値)で求めます。

>>> from sklearn.metrics import mean_absolute_error as MAE
>>> y_true = [10, 15, 12]
>>> y_pred = [12, 10, 10]
>>> MAE(y_true, y_pred)
3

3が求まりました。

RMSE（Root Mean Squared Error）

実測値と予測値の「誤差の2乗」から算出する指標です。
「平均平方二乗誤差」と呼ばれ、予測精度は0に近いほど高いと言えます。

RMSEの計算式

計算式は、全データの「実測値-予測値」の2乗の平均を計算し、最後に平方根を取ったものです。

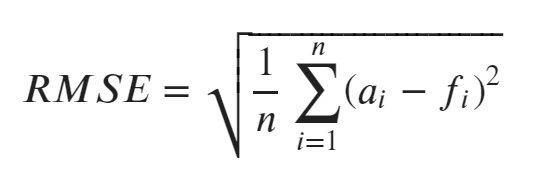
RMSEの計算例

誤差の2乗なのでMSEより数値が大きくなっています。
計算式に当てはめてみましょう。

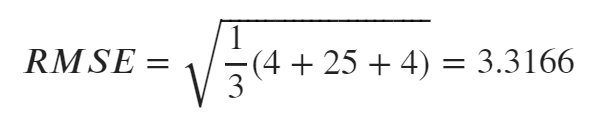
RMSE＝3.3166となりました。

sklearnを使ったRMSEの求め方

sklearnにはRMSEを求める関数は用意されていません。
しかし、関数の組み合わせにより簡単に求められます。

1. sklearn.metrics.mean_squrared_error()—MSEの算出
2. numpy.sqrt()—平方根の計算

この2つを使います。RMSEはMSEの値を平方根で補正したものです。
ですので、MSEを求めた後に平方根の計算を行えばRMSEを求めれます。

>>> from sklearn.metrics import mean_squared_error as MSE
>>> import numpy as np
>>> y_true = [10, 15, 12]
>>> y_pred = [12, 10, 10]
>>> np.sqrt(MSE(y_true, y_pred))
3.3166247903554

3.3166が求まりました。

MAEとRMSEの使い分け

RMSEは評価関数算出の際に、2乗しているためMAEに比べ大きく予測を外すと大きく悪い評価を与えます。

つまり、大きな予測誤差を出さず外れ値も出来るだけ当てたいようなモデルの場合にはRMSEのほうが有効といえます。

全サンプルの誤差が一定の場合、MAEとRMSEの数値に大きな差は出ません。
しかし、部分的に大きな誤差が生じている場合や大きな外れ値が存在する場合にRMSEは悪い評価になります。

このように使い分けを行います。

誤差率を測る評価関数—MAPE

MAPE（Mean Absolute Percentage Error）

実測値と予測値の誤差率（相対誤差）を算出する指標です。
「平均絶対パーセント誤差」と呼ばれ、予測精度は0％に近いほど高いと言えます。

MAEやRMSEが誤差の大きさで評価したのに比べ、MAPEは割合で評価するためスケールが異なるデータの誤差を比較しやすいことが特徴といえます。

ただし、実測値に０が含まれる場合は使用できません。

MAPEの計算式

計算式は、全データの「実測値-予測値」の絶対値の合計をn個で割った後に、100を乗じてパーセント単位にします。

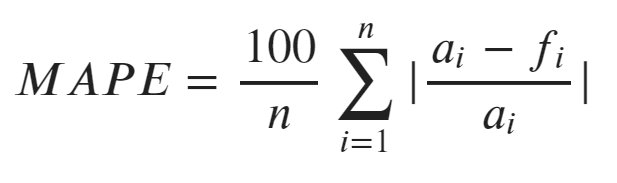
MAPEの計算例

上記データを計算式に当てはめると

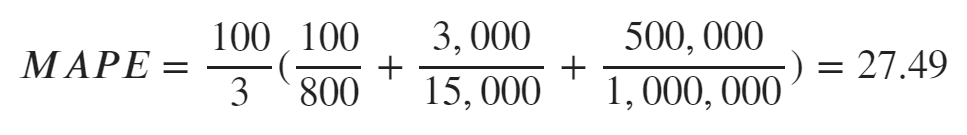
27.49%となります。試しにMAEで計算してみると、値は167700.0円となりました。
MAEの場合はスケールの大きい値に引っ張られて誤差の値が大きくなっています。

しかし、MAPEの場合は割合が算出されているため価格の大きさに影響されず誤差の割合を示しています。

このようにMAPEは誤差の割合で示すため、直感的に理解しやすい形式とも言えます。

前述しましたが、実測値に0が存在している場合にはMAPEは使えません。
先ほどの計算式を見てみると

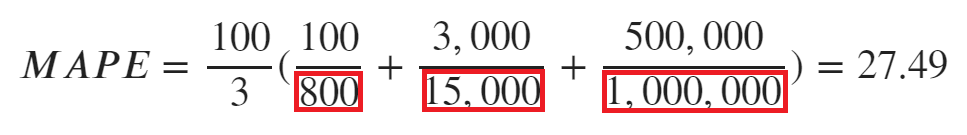
赤枠の部分が実測値となるため、0になると計算が出来なくなってしまうのです。
注意しましょう。

numpyを使ったMAPEの求め方

numpyの関数を組み合わせて簡単に求めることができます。
サンプルとして関数を作成しました。予測値・実測値を渡すことで計算できます。

>>> import numpy as np
>>> y_true = [800, 15000, 1000000]
>>> y_pred = [700, 12000, 1500000]

>>> def mean_absolute_percentage_error(y_true, y_pred):
        y_true, y_pred = np.array(y_true), np.array(y_pred)
        return np.mean(np.abs((y_pred - y_true) / y_true)) * 100

>>> mean_absolute_percentage_error(y_true, y_pred)

27.499999999999996

モデルの適合性を測る—R²

R²（決定係数; coefficient of determination）

モデルの当てはまりの良さを示す指標です。
「データそのもののバラつき」と「予測値のズレ」をもとに算出されます。

最も適合性が高い場合には1となり、つまり１に近ければ近いほど良いスコアといえます。

R²の計算式

１から「誤差の二乗」を「実測値-平均値の二乗」で割った平均値を引いたものになります。

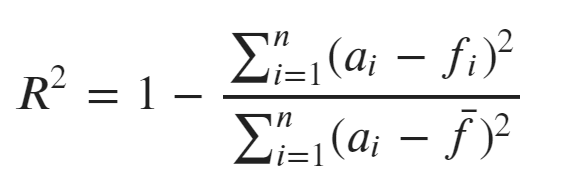
R²の計算例

ここでは「誤差が大きい場合・小さい場合」両方から見ていきます。
誤差が小さい場合から見ていきましょう。

こちらを計算すると

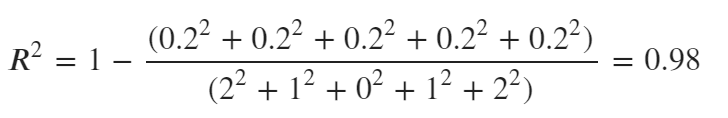
R²は0.98となりました。MAEの場合は0.2となります。
一方で部分的に外れ値（大きく値を外している）がある場合はどうなるのでしょうか。

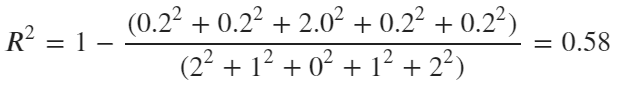
R²は0.58となり、MAEは0.56となりました。
MAEに大きな変化は見られませんでしたが、R²は大きく値が変化しました。

つまり、予測値と実測値が大きく外れる（モデルの適合性の悪化）場合には決定係数が下がることが分かりました。

sklearnを使ったR²の求め方

sklearnにはR²を求める関数が用意されています。

sklearn.metricsからr2_scoreをインポートし
r2_score(実測値, 予測値)で求めます。

>>> from sklearn.metrics import r2_score
>>> y_true = [2,3,4,5,6]
>>> y_pred = [2.2,3.2,4.2,5.2,6.2]
>>> r2_score(y_true, y_pred)
0.98

この記事のサンプルコード

機械学習・データ処理を学ぶのにおすすめの教材

じっくり書籍で学習するなら！

Python実践データ分析100本ノック

¥318 （2024/11/08 18:48時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ

Python 実践データ加工/可視化 100本ノック

¥830 （2024/11/11 16:04時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ

Kaggleで勝つデータ分析の技術

¥3,608 （2024/11/10 16:43時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ

Pythonデータ分析／機械学習のための基本コーディング！ pandasライブラリ活用入門 impress top gearシリーズ

¥2,090 （2022/02/20 08:45時点 | Amazon調べ）

Amazon

楽天市場

Yahooショッピング

ポチップ